binary search tree visualization

Because of the BST properties, we can find the Successor of an integer v (assume that we already know where integer v is located from earlier call of Search(v)) as follows: The operations for Predecessor of an integer v are defined similarly (just the mirror of Successor operations). This visualization is a Binary Search Tree I built using JavaScript. The idea of binary search is to use the information that the array is sorted and reduce the time complexity to O (Log n). Level-Order. You can recursively check BST property on other vertices too. WebBinary Search Tree, AVL Tree - VisuAlgo 1x Visualisation Scale Create Search Insert Remove Predec-/Succ-essor Tree Traversal > We use cookies to improve our website. Find the Successor(v) 'next larger'/Predecessor(v) 'previous smaller' element. Introduction A Binary Search Tree (BST) is a binary tree in which each vertex has only up to 2 children that satisfies BST property: All vertices in the left subtree of a vertex must hold a value smaller than its own and all vertices in the right subtree of a vertex must hold a value larger than its own (we have assumption that all values are distinct and var gcse = document.createElement('script'); On the example BST above, height(11) = height(32) = height(50) = height(72) = height(99) = 0 (all are leaves). Kevin Wayne. Visualization of Basic Terminology of Binary Search Trees. The properties of a binary search tree are recursive: if we consider any node as a root, these properties will remain true. An example of this would look something like this: Lets also look at some extra methods, findMin and contains, they are direct if you This pattern is the same no matter which node you look at. When you are ready to continue with the explanation of balanced BST (we use AVL Tree as our example), press [Esc] again or switch the mode back to 'e-Lecture Mode' from the top-right corner drop down menu. 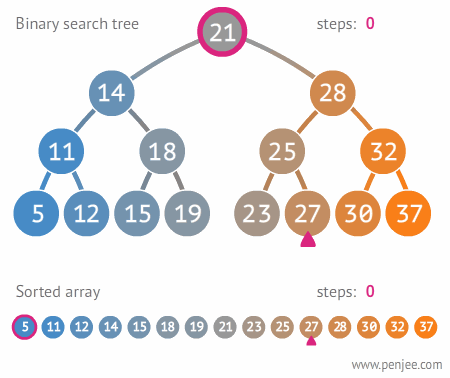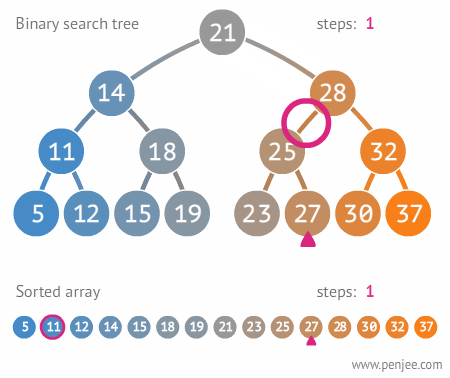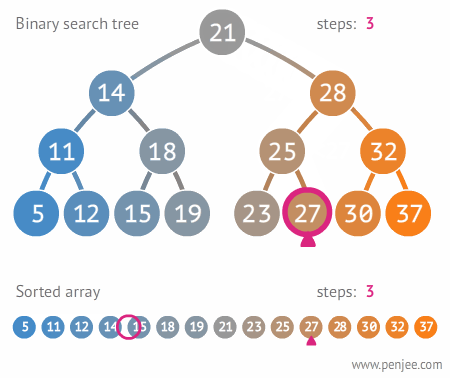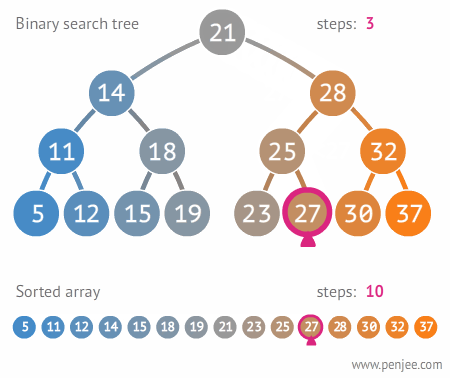rotateRight(T)/rotateLeft(T) can only be called if T has a left/right child, respectively. Last modified on August 26, 2016. WebThe binarysearch website currently does not support a binary tree visualization tool that exists in other sites like LeetCode. VisuAlgo is free of charge for Computer Science community on earth. We can also represent data in a ranked order using a binary tree. The right subtree of a node contains only nodes with keys greater than the nodes key. Disclosure to all visitors: We currently use Google Analytics to get an overview understanding of our site visitors. This part is also clearly O(1) on top of the earlier O(h) search-like effort. Try Search(100) (this value should not exist as we only use random integers between [1..99] to generate this random BST and thus the Search routine should check all the way from root to the only leaf in O(N) time not efficient. It has very fast Search(v), Insert(v), and Remove(v) performance (all in expected O(1) time). height(29) = 1 as there is 1 edge connecting it to its only leaf 32. Your user account will be purged after the conclusion of the module unless you choose to keep your account (OPT-IN). WebIn computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. See the example shown above for N = 15 (a perfect BST which is rarely achievable in real life try inserting any other integer and it will not be perfect anymore). Vertices that are not leaf are called the internal vertices. intentando acceder se encuentra fuera de servicio temporalmente debido a un What Is a Binary Search Tree Used For? Program: Write a program to perform operations of Binary Search tree in C++. Notice that only a few vertices along the insertion path: {41,20,29,32} increases their height by +1 and all other vertices will have their heights unchanged. | Binary Search Tree is a node-based binary tree data structure which has the following properties: The left subtree of a node contains only nodes with keys lesser than the nodes key. Skip the tedious work of setting up test data, and dive straight into practising your algorithms.

We have now see how AVL Tree defines the height-balance invariant, maintain it for all vertices during Insert(v) and Remove(v) update operations, and a proof that AVL Tree has h < 2 * log N. Therefore, all BST operations (both update and query operations except Inorder Traversal) that we have learned so far, if they have time complexity of O(h), they have time complexity of O(log N) if we use AVL Tree version of BST. Due to the way nodes in a binary search tree are ordered, an in-order traversal (left node, then root node, then right node) will always produce a sequence of values in increasing numerical order. Discussion: Is there other tree rotation cases for Insert(v) operation of AVL Tree? The right subtree of a node contains only nodes with keys greater than the nodes key.

Removing v without doing anything else will disconnect the BST. However, you can use zoom-in (Ctrl +) or zoom-out (Ctrl -) to calibrate this.