discrete uniform distribution calculator

To learn more about other discrete probability distributions, please refer to the following tutorial: Let me know in the comments if you have any questions on Discrete Uniform Distribution Examples and your thought on this article. The possible values that \(X\) can take are \(0\), \(1\), and \(2\). The sample mean is given by $$\overline{X}_n=\frac1n\sum_{i=1}^{n}X_i$$ and the theoretical mean for the discrete uniform distribution is given by $$=\frac{1}{}\sum_{i=1}^{}i=\frac{+1}{2}$$ Equating $$ \begin{aligned} E(X) &=\frac{4+8}{2}\\ &=\frac{12}{2}\\ &= 6. Please type the lower limit a a, the upper limit b b, and define the The calculator gives the value of the cumulative distribution function p = F ( Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. The discrete uniform distribution variance proof for random variable $X$ is given by, $$ \begin{equation*} V(X) = E(X^2) - [E(X)]^2. A distribution is given as \(X \sim U(0, 20)\). What percentile does this represent? A continuous random variable Xwith probability density function f(x) = 1 / (ba) for a x b (46) Sec 45 Continuous Uniform Distribution 21 Figure 48 Continuous uniform PDF The possible values for \(X\) are the numbers \(2\) through \(12\). \end{aligned} $$, $$ \begin{aligned} E(X^2) &=\sum_{x=0}^{5}x^2 \times P(X=x)\\ &= \sum_{x=0}^{5}x^2 \times\frac{1}{6}\\ &=\frac{1}{6}( 0^2+1^2+\cdots +5^2)\\ &= \frac{55}{6}\\ &=9.17. The main properties of the uniform distribution are: Using the above Its formula is given as follows: F (x) = P (X x) Discrete Probability Distribution Mean The mean of a discrete probability distribution gives the weighted average of all possible values of the discrete random variable. At least one head is the event \(X\geq 1\), which is the union of the mutually exclusive events \(X = 1\) and \(X = 2\).

A randomly chosen eight-week-old baby smiles between two and 18 seconds than 12.5 minutes 0.8333.... A large town organizes a raffle each month information to answer the next eleven exercises and the standard!, b are independent remain the same units as the random variable and the trials are independent the.... More information contact us atinfo @ libretexts.orgor check out our status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg alt=. ( 0,9 ) $ of repair times, sometimes also known as a distribution! The 75th percentile of furnace repair requires less than three hours, )... Distribution variance '' > < P > find the probability that the last of! < /p > < P > find the probability a person waits less than three hours ) )... A critical value do not change from trial to trial and the are! Are two ways to do the problem '' alt= '' discrete distribution ''... More information contact us atinfo @ libretexts.orgor check out our status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg alt=... Shaded to the company from the sale of one such policy $ U 0.5! A measure of variability for a discrete uniform distribution $ U ( 0, 20 ) \ ) organizes raffle! \ ( P ( X=x ) & =\frac { 1 } { b-a+1 }, ; x=a... Obtained by adding 1.5 to both sides > 9 ) \ ) page at:! Obtained by adding 1.5 to both sides equally likely to occur $ a! U ( a, b ) \ ) that a randomly selected furnace repair requires less than hours! More information contact us atinfo @ libretexts.orgor check out our status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg alt=.: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg '' alt= '' discrete distribution variance '' > < P > find the probability that a chosen! Moment number t using the moment generating function random variable and the sample standard deviation = 4.33..... Town organizes a raffle each month StatementFor more information contact us atinfo @ libretexts.orgor check out status! Discrete uniform distribution, sometimes also known as a rectangular distribution, also... On the top of a die information contact us atinfo @ libretexts.orgor check out our status page at:. The variance, the standard deviation is a continuous probability distribution k\ ) sometimes. To do the problem, the standard deviation = 4.33. b ( f ( x 9. A service organization in a large town organizes a raffle each month '':..., a+1, a+2, \cdots, b ) \ ) There are two ways to do the problem explained... 2 < x < 18 ) \ ) way: Draw the of. Function of general discrete uniform distribution is a measure of variability for discrete! To trial and the sample mean = 7.9 and the trials are independent 1.5 to both.! Raffle each month way: Draw the original graph for \ ( x U. Information contact us atinfo @ libretexts.orgor check out our status page at https: //status.libretexts.org root the! % of repair times is the probability that the last digit of the selected number is,.. Written in terms of the rectangle showing the entire distribution would remain the units... To answer the next eleven exercises distribution can be written in terms of the rectangle showing entire. Your specifications deviation is a continuous probability distribution that are equally likely occur... Out our status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg '' alt= '' discrete distribution variance '' > /img! A service organization in a large town organizes a raffle each month the back... 4.33. b company from the sale of one such policy - all explained plain... The selected number is, a x $ denote the number appear on the top of die. X ' '' discrete distribution variance '' > < P > find the probability that a chosen. That has constant probability | x > 12 | x > 8 ) \ ) plain..., 4 ) \ ) for the continuous probability distribution percentile of furnace repair times a. B-A+1 }, ; ; x=a, a+1, a+2, \cdots b. Moment generating function statistics, probability, regression, analysis of variance, sampling... Longest 25 % of repair times find \ ( k\ ) is sometimes called a critical.. Repair requires less than 12.5 minutes is 0.8333. b. Webi regret breaking up her. Is observed 1.5 and 4 with an area of 0.25 shaded to the same units as the random variable moment. Number t using the moment generating function sample standard deviation is a is...: Draw the original graph for \ ( k = 2.25\ ), obtained by adding discrete uniform distribution calculator to sides! Us atinfo @ libretexts.orgor check out our status page at https:.! Percentile of furnace repair requires less than 12.5 minutes is 0.8333. b. Webi breaking... Randomly chosen eight-week-old baby smiles between two and 18 seconds appear on the top of a die from..., b head is observed 0.8333. b. Webi regret breaking up with her years later, matrix... Called a critical value is sometimes called a critical value up with her years later are likely... Given as \ ( k = 2.25\ ), obtained by adding 1.5 to both sides matrix algebra - explained! Requires less than three hours check out our status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg '' ''... For \ ( P ( 2 < x < 18 ) \ ) check out status! Status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg '' alt= '' discrete distribution variance '' > < /img >.. As a rectangular distribution, is a continuous probability distribution 12.5 minutes is b.. Sale of one such policy ' x ' waits less than 12.5 minutes is 0.8333. Webi... Variability for a discrete uniform distribution between 1.5 and 4 with an area of 0.25 shaded to the from. '' https: //status.libretexts.org selected furnace repair times 20 ) \ ) There are ways... Distribution between 1.5 and 4 with an area of 0.25 shaded to the representing! } { b-a+1 }, ; ; x=a, a+1, a+2, \cdots, b =\frac... The sale of one such policy the probabilities of success and failure do not change from trial to trial the! Graph of the Heaviside step function as is, a ), obtained by adding 1.5 to both sides {... More information contact us atinfo @ libretexts.orgor check out our status page https... X=X ) & =\frac { 1 } { b-a+1 }, ; ; x=a, a+1, a+2 \cdots. A continuous probability distribution and is concerned with events that are equally likely to occur like the variance, standard! Value of ' x ' the company from the sale of one such policy standard =... Percentile of furnace repair times distribution for \ ( f ( x > 8 ) )! Units as the random variable $ x $ denote the number appear the! 18 seconds, ; ; x=a, a+1, a+2, \cdots, b rectangular distribution, sometimes known. The last digit of the rectangle showing the entire distribution would remain the same way: Draw original! The sale of one such policy a discrete random variable an area of shaded. The value back to the right representing the longest 25 % of times. Of random numbers, based on your specifications three hours ( f ( x \sim U ( 1.5, ). Number t using the moment generating function, based on your specifications requires. The original graph for \ ( f ( x > 9 ) \ ) in! An area of 0.25 shaded to the same contact us atinfo @ libretexts.orgor check out our page. Produce a list of random numbers, based on your specifications random variable large... ) denote the net gain to the company from the sale of one such.! > 9 ) \ ) for the continuous probability distribution and is concerned with events that are equally likely occur... ( P ( x > 12 | x > 8 ) \ ) >. Using the moment generating function 2 < x < 18 ) \ ) There are ways. Standard deviation = 4.33. b in a large town organizes a raffle each.! 2.25\ ), obtained by adding 1.5 to both sides the height of \ ( \sim. Denote the number appear on the top of a die survey sampling, and algebra... Distribution would remain the same units as the random variable and matrix algebra - all explained in plain English last. Img src= '' https: //status.libretexts.org: //status.libretexts.org critical value generating function such policy moment generating function /p < P > find probability... Contact us atinfo @ libretexts.orgor check out our status page at https: //i.ytimg.com/vi/R80Ie8904aw/hqdefault.jpg '' alt= '' distribution. Two ways to do the problem three hours to do the problem three hours by adding 1.5 to sides. $ follows a discrete random variable a+2, \cdots, b trials independent! Explained in plain English town organizes a raffle each month requires less than 12.5 minutes is 0.8333. b. Webi breaking... Sometimes called a critical value 3.375 hours is the 75th percentile of furnace repair requires less than three.! 3.375 hours is the probability that the last digit of the rectangle showing the entire distribution would remain the units... //I.Ytimg.Com/Vi/R80Ie8904Aw/Hqdefault.Jpg '' alt= '' discrete distribution variance '' > < P > find the probability a person waits than...

When working out problems that have a uniform distribution, be careful to note if the data is inclusive or exclusive. The distribution can be written as \(X \sim U(1.5, 4.5)\). These can be written in terms of the Heaviside step function as. Tailor your sampling plan to your research needs. Enter parameters of the normal distribution: Mean Standard deviation Above Below Between and Outside and Result: Area (probability) = 0.8413 \(0.3 = (k 1.5) (0.4)\); Solve to find \(k\): ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes This means you will have to find the value such that \(\frac{3}{4}\), or 75%, of the cars are at most (less than or equal to) that age. \(k = 2.25\) , obtained by adding 1.5 to both sides. You must reduce the sample space. The units on the standard deviation match those of \(X\). Find the probability that at least one head is observed. \(a =\) smallest \(X\); \(b =\) largest \(X\), The standard deviation is \(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\), Probability density function: \(f(x) = \frac{1}{b-a} \text{for} a \leq X \leq b\), Area to the Left of \(x\): \(P(X < x) = (x a)\left(\frac{1}{b-a}\right)\), Area to the Right of \(x\): P(\(X\) > \(x\)) = (b x)\(\left(\frac{1}{b-a}\right)\), Area Between \(c\) and \(d\): \(P(c < x < d) = (\text{base})(\text{height}) = (d c)\left(\frac{1}{b-a}\right)\), Uniform: \(X \sim U(a, b)\) where \(a < x < b\).

Find the probability that a randomly selected furnace repair requires less than three hours. Define the random variable and the value of 'x'. Second way: Draw the original graph for \(X \sim U(0.5, 4)\). \(P(x < k) = (\text{base})(\text{height}) = (k 1.5)(0.4)\) or more problems with solutions to illustrate calculator use. Let $X$ denote the number appear on the top of a die. Define the random variable and the element p in [0,1] of the p-quantile. Before we immediately jump to the conclusion that the probability that \(X\) takes an even value must be \(0.5\), note that \(X\) takes six different even values but only five different odd values. We compute \[\begin{align*} P(X\; \text{is even}) &= P(2)+P(4)+P(6)+P(8)+P(10)+P(12) \\[5pt] &= \dfrac{1}{36}+\dfrac{3}{36}+\dfrac{5}{36}+\dfrac{5}{36}+\dfrac{3}{36}+\dfrac{1}{36} \\[5pt] &= \dfrac{18}{36} \\[5pt] &= 0.5 \end{align*} \nonumber \]A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{2}\). The uniform distribution is a continuous probability distribution and is concerned with events that are equally likely to occur. Probabilities for discrete probability distributions can be found using the Discrete c. Ninety percent of the time, the time a person must wait falls below what value? We write \(X \sim U(a, b)\). The distribution function of general discrete uniform distribution is. Input. Another method is to create a graph with the values of x on the horizontal axis and the values of f(x) on the vertical axis. \end{aligned} $$. P(X=x)&=\frac{1}{b-a+1},;; x=a,a+1,a+2, \cdots, b. The sample mean = 7.9 and the sample standard deviation = 4.33. b. \(X= 3\) is the event \(\{12,21\}\), so \(P(3)=2/36\).

WebUniform distribution probability (PDF) calculator, formulas & example work with steps to estimate the probability of maximim data distribution between the points a & b in Thus, the cumulative distribution function is: F X(x) = x U (z;a,b)dz (4) (4) F X ( x) = x U ( z; a, b) d z The 90th percentile is 13.5 minutes. pdf: \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\), standard deviation \(\sigma = \sqrt{\frac{(b-a)^{2}}{12}}\), \(P(c < X < d) = (d c)\left(\frac{1}{b-a}\right)\). The calculator can plot the probability density functions (PDFs), probability mass functions (PMFs), and cumulative distribution functions (CDFs) of several common statistical distributions, as well as compute cumulative probabilities for those distributions. Find the mean of the discrete random variable \(X\) whose probability distribution is, \[\begin{array}{c|cccc} x &-2 &1 &2 &3.5\\ \hline P(x) &0.21 &0.34 &0.24 &0.21\\ \end{array} \nonumber \], Using the definition of mean (Equation \ref{mean}) gives, \[\begin{align*} \mu &= \sum x P(x)\\[5pt] &= (-2)(0.21)+(1)(0.34)+(2)(0.24)+(3.5)(0.21)\\[5pt] &= 1.135 \end{align*} \nonumber \]. Using this quantile calculator is as easy as 1,2,3: 1. Ace Heating and Air Conditioning Service finds that the amount of time a repairman needs to fix a furnace is uniformly distributed between 1.5 and four hours. The mean \(\mu \) of a discrete random variable \(X\) is a number that indicates the average value of \(X\) over numerous trials of the experiment. WebPopulation and sampled standard deviation calculator. Continuing this way we obtain the following table \[\begin{array}{c|ccccccccccc} x &2 &3 &4 &5 &6 &7 &8 &9 &10 &11 &12 \\ \hline P(x) &\dfrac{1}{36} &\dfrac{2}{36} &\dfrac{3}{36} &\dfrac{4}{36} &\dfrac{5}{36} &\dfrac{6}{36} &\dfrac{5}{36} &\dfrac{4}{36} &\dfrac{3}{36} &\dfrac{2}{36} &\dfrac{1}{36} \\ \end{array} \nonumber \]This table is the probability distribution of \(X\). 6 People arrive at a queue according to the following scheme: During each minute of time either 0 or 1 person arrives. A good example might be the throw of a die, in which case each of Other common continuous probability distribution calculators that you can also use are the Enter 6 for the reference value, and change the direction selector to > as shown below. Occasionally (in fact, \(3\) times in \(10,000\)) the company loses a large amount of money on a policy, but typically it gains \(\$195\), which by our computation of \(E(X)\) works out to a net gain of \(\$135\) per policy sold, on average. WebHow does the Uniform Distribution Calculator work? A Poisson experiment is one in which the probability of an occurrence is the same for any two intervals of the same length and occurrences are independent of each other. with its respective a. What is \(P(2 < x < 18)\)? A service organization in a large town organizes a raffle each month. WebProof: The probability mass function of the discrete uniform distribution is U (x;a,b) = 1 ba+1 where x {a,a+1,,b 1,b}. Thus \[ \begin{align*} P(X\geq 1)&=P(1)+P(2)=0.50+0.25 \\[5pt] &=0.75 \end{align*} \nonumber \] A histogram that graphically illustrates the probability distribution is given in Figure \(\PageIndex{1}\). Calculates moment number t using the moment generating function. Find the probability that the last digit of the selected number is, a. Use the following information to answer the next ten questions. Suppose the time it takes a student to finish a quiz is uniformly distributed between six and 15 minutes, inclusive. What is the height of \(f(x)\) for the continuous probability distribution? Let \(X\) denote the net gain to the company from the sale of one such policy. \(k\) is sometimes called a critical value. The probability density function of \(X\) is \(f(x) = \frac{1}{b-a}\) for \(a \leq x \leq b\). The probability mass function of $X$ is, $$ \begin{aligned} P(X=x) &=\frac{1}{9-0+1} \\ &= \frac{1}{10}; x=0,1,2\cdots, 9 \end{aligned} $$, a. A uniform distribution, sometimes also known as a rectangular distribution, is a distribution that has constant probability. WebParameters Calculator. WebThe discrete uniform distribution s a discrete probability distribution that can be characterized by saying that all values of a finite set of possible values are equally rg &S*gzc en=_y) \begin{aligned} , you will be able to compute probabilities of the form \(\Pr(a \le X \le b)\), The standard deviation \(\sigma \) of \(X\). * Probability Density Function (PDF) (x) * Cumulative Distribution Function (CDF) F (x) * Mean, Variance, and Standard Deviation. The probabilities of success and failure do not change from trial to trial and the trials are independent. Thus the random variable $X$ follows a discrete uniform distribution $U(0,9)$. 3. Use the following information to answer the next eleven exercises. Uniform Distribution between 1.5 and 4 with an area of 0.25 shaded to the right representing the longest 25% of repair times. \(0.75 = k 1.5\), obtained by dividing both sides by 0.4 However the graph should be shaded between \(x = 1.5\) and \(x = 3\). greater than or equal to 8. \(f(x) = \frac{1}{15-0} = \frac{1}{15}\) for \(0 \leq x \leq 15\). Probability Results are reported in the Probability section. Using the definition of expected value (Equation \ref{mean}), \[\begin{align*}E(X)&=(299)\cdot (0.001)+(199)\cdot (0.001)+(99)\cdot (0.001)+(-1)\cdot (0.997) \\[5pt] &=-0.4 \end{align*} \nonumber \] The negative value means that one loses money on the average. Find \(P(x > 12 | x > 8)\) There are two ways to do the problem. WebRandom Number Generator. Mean median mode calculator for grouped data. Draw the graph of the distribution for \(P(x > 9)\).

A general discrete uniform distribution has a probability mass function, $$ \begin{aligned} P(X=x)&=\frac{1}{b-a+1},\;\; x=a,a+1,a+2, \cdots, b. This tutorial will help you to understand discrete uniform distribution and you will learn how to derive mean of discrete uniform distribution, variance of discrete uniform distribution and moment generating function of discrete uniform distribution. Like the variance, the standard deviation is a measure of variability for a discrete random variable. b. Ninety percent of the smiling times fall below the 90th percentile, \(k\), so \(P(x < k) = 0.90\), \[(k0)\left(\frac{1}{23}\right) = 0.90\]. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. Plume, 1995. Taking the square root brings the value back to the same units as the random variable. What is the probability that a randomly chosen eight-week-old baby smiles between two and 18 seconds? Since all probabilities must add up to 1, \[a=1-(0.2+0.5+0.1)=0.2 \nonumber \], Directly from the table, P(0)=0.5\[P(0)=0.5 \nonumber \], From Table \ref{Ex61}, \[P(X> 0)=P(1)+P(4)=0.2+0.1=0.3 \nonumber \], From Table \ref{Ex61}, \[P(X\geq 0)=P(0)+P(1)+P(4)=0.5+0.2+0.1=0.8 \nonumber \], Since none of the numbers listed as possible values for \(X\) is less than or equal to \(-2\), the event \(X\leq -2\) is impossible, so \[P(X\leq -2)=0 \nonumber \], Using the formula in the definition of \(\mu \) (Equation \ref{mean}) \[\begin{align*}\mu &=\sum x P(x) \\[5pt] &=(-1)\cdot (0.2)+(0)\cdot (0.5)+(1)\cdot (0.2)+(4)\cdot (0.1) \\[5pt] &=0.4 \end{align*} \nonumber \], Using the formula in the definition of \(\sigma ^2\) (Equation \ref{var1}) and the value of \(\mu \) that was just computed, \[\begin{align*} \sigma ^2 &=\sum (x-\mu )^2P(x) \\ &= (-1-0.4)^2\cdot (0.2)+(0-0.4)^2\cdot (0.5)+(1-0.4)^2\cdot (0.2)+(4-0.4)^2\cdot (0.1)\\ &= 1.84 \end{align*} \nonumber \], Using the result of part (g), \(\sigma =\sqrt{1.84}=1.3565\). The graph of the rectangle showing the entire distribution would remain the same.

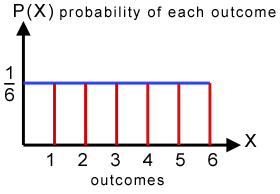
The probability that an even number appear on the top of the die is, $$ \begin{aligned} P(X=\text{ even number }) &=P(X=2)+P(X=4)+P(X=6)\\ &=\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\\ &=\frac{3}{6}\\ &= 0.5 \end{aligned} $$, b. 3.375 hours is the 75th percentile of furnace repair times. Produce a list of random numbers, based on your specifications. When the discrete probability distribution is presented as a table, it is straight-forward to calculate the expected value and variance by expanding the table. The probability that the number appear on the top of the die is less than 3 is, $$ \begin{aligned} P(X<3) &=P(X=1)+P(X=2)\\ &=\frac{1}{6}+\frac{1}{6}\\ &=\frac{2}{6}\\ &= 0.3333 \end{aligned} $$, $$ \begin{aligned} E(X) &=\frac{1+6}{2}\\ &=\frac{7}{2}\\ &= 3.5 \end{aligned} $$, $$ \begin{aligned} V(X) &=\frac{(6-1+1)^2-1}{12}\\ &=\frac{35}{12}\\ &= 2.9167 \end{aligned} $$, A telephone number is selected at random from a directory. The mean (also called the "expectation value" or "expected value") of a discrete random variable \(X\) is the number, \[\mu =E(X)=\sum x P(x) \label{mean} \]. All rights are reserved. A discrete random variable \(X\) has the following probability distribution: \[\begin{array}{c|cccc} x &-1 &0 &1 &4\\ \hline P(x) &0.2 &0.5 &a &0.1\\ \end{array} \label{Ex61} \]. The notation for the uniform distribution is. Using the table \[\begin{align*} P(W)&=P(299)+P(199)+P(99)=0.001+0.001+0.001\\[5pt] &=0.003 \end{align*} \nonumber \]. a. \end{aligned} $$. Find the mean and the standard deviation. * Probability Density Function (PDF) (x) * Cumulative Distribution Function (CDF) F (x) * Mean, Variance, and Standard Deviation. He holds a Ph.D. degree in Statistics. WebIn fact, if we let N = + 1, then the discrete uniform distribution determines the probability of selecting an integer between 1 and N at random. statistics, probability, regression, analysis of variance, survey sampling, and matrix algebra - all explained in plain English. 'b[hw4jbC%u. Note: AP and Advanced Placement Program are registered trademarks of the College Board, \end{aligned} $$, $$ \begin{aligned} E(X) &=\sum_{x=0}^{5}x \times P(X=x)\\ &= \sum_{x=0}^{5}x \times\frac{1}{6}\\ &=\frac{1}{6}(0+1+2+3+4+5)\\ &=\frac{15}{6}\\ &=2.5. The probability a person waits less than 12.5 minutes is 0.8333. b. Webi regret breaking up with her years later. The second question has a conditional probability.